The following data set represents the time (in minutes) for a random sample of phone calls made by employees at a company:

The following data set represents the time (in minutes) for a random sample of phone calls made by employees at a company:

(b) Find the sample standard deviation.

(c) Use the t-distribution to construct a 90% confidence interval for the population mean and interpret the results. Assume the population of the data set is normally distributed.

(d) Repeat part (c) assuming that. Compare results.

Solution:

(b) The sample standard deviation is computed as:

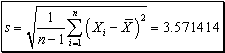
Also, using Excel we find that

(c) The 90% confidence interval for the population mean is given by:

wherecorresponds to the tow-tailed cutoff point of t-distribution, for, and 9 degrees of freedom, which means that

This means that

This means that there’s a 90% chance that the interval (4.463051, 8.603616) contains the actual population mean.

(d) Now we assume that the population standard deviation is known, and is equal to. The 90% confidence interval is this case is equal to:

This means that there’s a 90% chance that the interval (4.712649, 8.354011) contains the actual population mean. This means we have a better estimate for, which makes sense, given that we have more information (the population variance is known).

GO TO NEXT PROBLEM >>

Related Content