In New York state, savings banks are permitted to sell a form of life insurance called Savings Bank Life Insurance (SBLI)

In New York state, savings banks are permitted to sell a form of life insurance called Savings Bank Life Insurance (SBLI). The approval process consists of underwriting, which includes a review of the application, a medical information bureau check, possible requests for additional medical information and medical exams, and a policy compilation stage where the policy pages are generated and sent to the bank for delivery. The ability to deliver approved policies to customers in a timely manner is critical to the profitability of this service to the bank. During a period of 1 month, a random sample of 27 approved policies was selected INSURANCE and the total processing time in days recorded:

73 19 16 64 28 28 31 90 60 56 31

56 22 18 45 48 17 17 17 91 92 63

50 51 69 16 17

a. Construct a 95% confidence interval estimate of the mean processing time.

b. What assumption must you make about the population distribution in (a)?

c. Do you think that the assumption made in (b) is seriously violated? Explain.

Solution: a.-) This problem is similar to the previous problem, because we don’t have the population variance, so we have to use the t-student distribution. Again, we have that the formula for the confidence interval is:

where is the sample mean, is the sample variance, and corresponds to the symmetric cut-off of the tail of the t-student distribution with degrees of freedom. Since , then

With the help of EXCEL we can compute the following table:

Therefore,, and . So, we compute the confidence interval as

b.-) In order to use the t-student distribution we have to assume that the distribution of the total processing time is normally distributed.

c.-) To verify if the total processing time is normally distributed to some degree, we could draw an histogram. For normalizing purposes, we are going to work with the z-scores associated to the data.

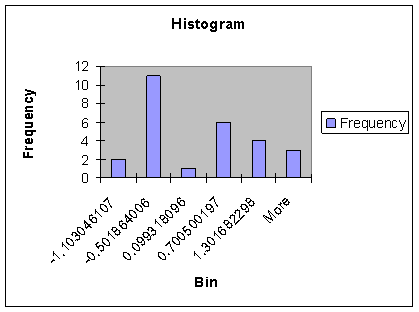
From the histogram it looks like the distribution is not much normal-like. But we cannot be conclusive if we don’t have more evidence. The assumption on b.-) might be not satisfied.

GO TO NEXT PROBLEM >>

Related Content