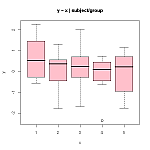
Calculate the means

a. Calculate the means
b. The MINITAB ANOVA printout is shown here. Test for interaction at the α = 0.05 level of significance.
Analysis of variance for response.

Solution: (a) We get
Level 1: ![]()
Level 2: ![]()
Level 3: ![]()
A: ![]()
B: ![]()
(b) We need to test for the significance of the interaction AB at the 0.05 level of significance. The F-statistics is equal to 1.48678, as we can see in the table above. The critical F value, at the 0.05 significance level, and 2, 6 degrees of freedom is equal to 5.1433. This means that we fail to reject the null hypothesis of no interaction between the variables.
c. Do the results warrant tests of the two factor mean effects?
Solution: Since from part b) we can assume that there's no interaction between the factors A and B, now we test for the significance of the main effects.
- Factor A: The F-statistics is equal to 0.11851. The critical F-value for
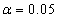 and 1, 6 degrees of freedom is 5.9874. This means that we fail to reject the null hypothesis of lack of significance of factor A
and 1, 6 degrees of freedom is 5.9874. This means that we fail to reject the null hypothesis of lack of significance of factor A
- Factor B: The F-statistics is equal to 0.55391. The critical F-value for
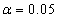 and 2, 6 degrees of freedom is 5.1433. This means that we fail to reject the null hypothesis of lack of significance of factor B
and 2, 6 degrees of freedom is 5.1433. This means that we fail to reject the null hypothesis of lack of significance of factor B
Related Content


The U.S. Weather Bureau has provided the following information about - StatisticsHelp
Statistics Help: Where To Find it? - StatisticsHelp

