If null hypothesis is rejected in this problem use Scheffe test if the sample sizes are unequal to test the differences betwee
If null hypothesis is rejected in this problem use Scheffe test if the sample sizes are unequal to test the differences between the means, and use the Tukey test if the sample sizes are equal. For this problem, state hypotheses and identify the claim, find the critical value(s), compute the test value, make the decision, summarize the results.
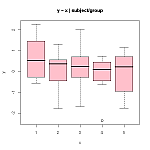
The weights in ounces of 4 types of women's shoes are shown here. At a=0.05 test the claim that there is no difference in the mean weights of the groups.

Solution: We need to test the following hypothesis
![]()
Using Statdisk we find the following results:
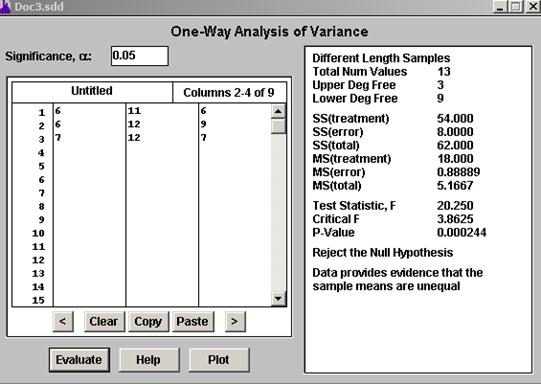
The F-test statistics is equal to
![]()
The critical value is found in the F-table, for (3, 9) degrees of freedom, and 0.05 significance level. Notice that the p-value is 0.000244, which is less than the significance level. That means that we reject the null hypothesis of equal means. Now we need to perform Scheffe or Tukey when it corresponds. We have the following output from SPSS
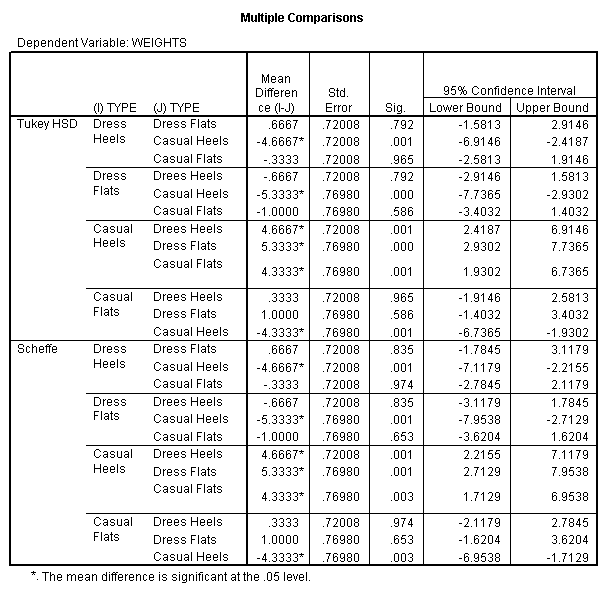
Using this table we find that “Casual Heels” have the largest mean weight of the groups, with 95% confidence. The rest of the mean are the same at the 0.05 significance level.
The Tukey confidence interval is computed as
![]()
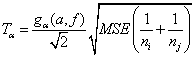
and![]() ,
,![]() ,
, ![]() , and
, and![]() is the upper
is the upper![]() percentage point of the studentized range statistics
percentage point of the studentized range statistics![]() , defined as
, defined as
![]() .
.
Related Content


Combining Efforts with a Statistics Expert - StatisticsHelp
Statistics Help: Where To Find it? - StatisticsHelp

