Students were paired by matching their IQs and grades in previous mathematics courses taken
Students were paired by matching their IQs and grades in previous mathematics courses taken. Group A attended lecture and did homework. Group B watched videotapes and did work on a computer. Test to see if there is a significant difference in final exam scores for 2 groups at the .05 level.
Lecture
95
87
91
85
81
79
74
73
71
69
Tapes
99
91
88
90
87
78
79
81
65
74
Solution: We have paired samples, so we have to use t-test for independent samples. We want to test the following hypotheses:
We need to compute the t-statistics for this 2-tailed test. Before that, we need to test to see if the variances can be considered the same. We use Excel to get
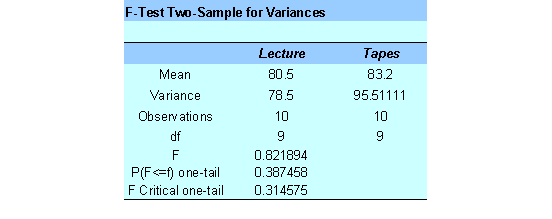
We see that the p-value is 0.387458, which is greater than the significance level
, and therefore we cannot reject the null hypothesis of equal variances.
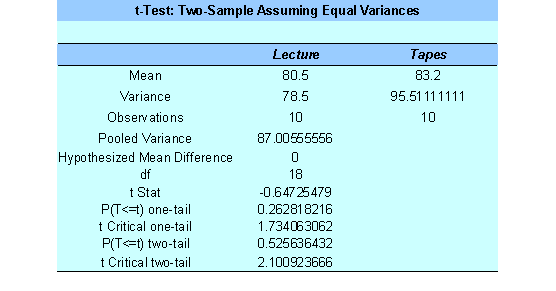
Now we test our main hypothesis assuming that the variances are equal. The t-statistics is found using Excel:
|
| ||
|
|
||
|
|
Lecture |
Tapes |
|
|
80.5 |
83.2 |
|
|
78.5 |
95.51111111 |
|
|
10 |
10 |
|
|
87.00555556 |
|
|
|
0 |
|
|
|
18 |
|
|
|
-0.64725479 |
|
|
|
0.262818216 |
|
|
|
1.734063062 |
|
|
|
0.525636432 |
|
|
|
2.100923666 |
|
We observe that the p-value is 0.5256, which is greater than the significance level, which means that we fail to reject the null hypothesis. In other words, we don’t have enough evidence to claim that there is a significant difference in final exam scores for 2 groups at the .05 level
Related Content
Combining Efforts with a Statistics Expert - StatisticsHelp
The U.S. Weather Bureau has provided the following information about - StatisticsHelp
