A cereal company claims that their new cereal boxes include at least 50g more cereal than their old boxes

A cereal company claims that their new cereal boxes include at least 50g more cereal than their old boxes. A consumer advocacy group tests this claim by weighing the contents of 70 randomly chosen old and new boxes of cereal. The mean weight for the new cereal boxes is 386g with a standard deviation of 12g, and the mean weight for the old boxes is 340g, with a standard deviation of 9g.

(a) State the null and alternative hypotheses.

(b)Perform the hypothesis test, using a p-value approach. What statement can the consumer advocacy group make about the cereal company’s claim?

c) Describe in words what is the Type I error for this test. What is the probability of Type I error given the type of test performed? Describe in words what the Type II error would be.

Solution: We need to test the following null and alternative hypotheses:

which corresponds to a left-tailed independent samples t-test. We can use normal approximation because both of the sample sizes are greater than or equal to 30. The z-statistics is computed as

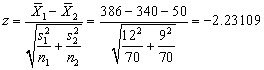
Using the p-value approach, the two-tailed p-value is computed as

Since the p-value is greater than the significance level, then we fail to reject the null hypothesis. This means that we don't have enough evidence to reject the claim that the new cereal boxes include at least 50g more cereal than their old boxes, at the 0.01 significance level. (We would reject the claim at the 0.05 significance level though)

The type I error would be to reject the null hypothesis (the cereal company claim in this case) when it is actually true. Since we chose a significance level of, the probability of type I error is 0.01. The type II error would be to fail to reject the claim of the cereal company when it is actually false)

GO TO NEXT PROBLEM >>

Related Content