
A production engineer claims that there is no difference in the mean nut
A production engineer claims that there is no difference in the mean nut
diameter manufactured by two different methods. The first method produces nuts with the following diameters (in centimeters).
|
3.33 |
3.337 |
3.329 |
3.354 |
3.325 |
3.343 |
3.333 |
3.347 |
3.332 |
3.358 |
|
3.353 |
3.335 |
3.341 |
3.331 |
3.327 |
3.326 |
3.337 |
3.336 |
3.323 |
3.347 |
|
3.329 |
3.345 |
3.329 |
3.338 |
3.353 |
3.339 |
3.338 |
3.338 |
3.35 |
3.32 |
|
3.364 |
3.34 |
3.348 |
3.339 |
3.336 |
3.321 |
3.316 |
3.352 |
3.32 |
3.336 |
![]()
The second method produces nuts with theses diameters (in centimeters).

Use an alpha level of .01 and test the hypothesis that the two methods are producing the same mean.
Solution: We have to use a (non-paired) t-test. First we analyze the variances with an F-test. The outcome from EXCEL is:
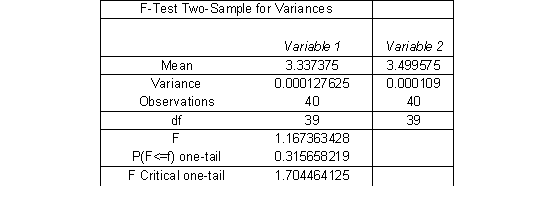
The p-value=2*0.315658=0.631 indicates that the difference is not significant, and we can assume equal variances.
Now we run a t-test (assuming equal variances). The EXCEL output follows:
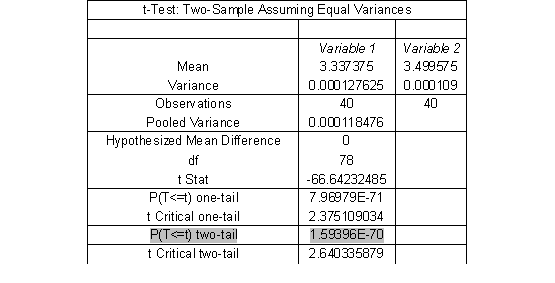
The p-value is 1.59396E-70, which is less than 0.01. That means that we reject the null hypothesis that the two methods are producing the same mean, at the 0.01 level of significance.
Related Content

Collection of Solved Statistics Problems - StatisticsHelp

The U.S. Weather Bureau has provided the following information about - StatisticsHelp

