A financial analyst is interested in estimating the average amount of a foreign loan by U
A financial analyst is interested in estimating the average amount of a foreign loan by U.S. banks. The analyst believes that the amount of a loan may be different depending on the bank, or, more precisely, on the extent of the bank’s involvement in foreign loans. The analyst obtains the following data on the percentage of profits of U.S. banks from loans to Mexico and proposes to use these data in the construction of stratum weights. The strata are the different banks: First Chicago, 33%; Manufacturers Hanover, 27%; Bankers Trust, 21%; Chemical Bank, 19%; Wells Fargo Bank, 19%;
Citicorp, 16%; Mellon Bank, 16%; Chase Manhattan, 15%; Morgan Guarantee Trust, 9%.
a. Construct the stratum weights for proportional allocation.
b. Discuss two possible problems with this study.
Solution: a. Proportional allocation means that the weight ![]() is such that
is such that
![]()
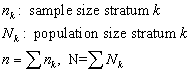
According with the design of the sampling, the sample size of the stratum k is 1, same as the population size of the stratum k. Therefore, for the strata we get that
![]()
b. Two possible problems with this study are:
1. It may not include all the banks to make the strata representative enough of the whole universe of U.S. banks.
2. The design of the strata involves having a sample size of 1, per strata. That’s not good in terms of statistical consistency. The whole idea of the stratified sampling is to reduce the “cost” of sampling by analyzing different strata, and strata are chosen to be homogeneous and mutually exclusive. For each stratum we apply the normal sampling method (usually random sampling) and based on the homogeneity of the strata we expect that the sample size required to get accurate estimates are not too big. But in terms of statistics consistency it is not a good idea to base an estimate on a sample of size 1.
Related Content

Statistics Help: Where To Find it? - StatisticsHelp

Combining Efforts with a Statistics Expert - StatisticsHelp