A quality characteristic of interest for a tea-bag-filling process is the weight of the tea in the individual bags

A quality characteristic of interest for a tea-bag-filling process is the weight of the tea in the individual bags. In this example, the label weight on the package indicates that the mean amount is 5.5 grams of tea in a bag. If the bags are underfilled, two problems arise. First, customers may not be able to brew the tea to be as strong as they wish. Second, the company may be in violation of the truth-in-labeling laws. On the other hand, if the mean amount of tea in a bag exceeds the label weight, the company is giving away product. Getting an exact amount of tea in a bag is problematic because of variation in the temperature and humidity inside the factory, differences in the density of the tea, and the extremely fast filling operation of the machine (approximately 170 bags a minute). The following table provides the weight in grams of a sample of 50 tea bags produced in one hour by a single machine. TEABAGS

Weight of Tea Bags in Grams

5.65 5.44 5.42 5.40 5.53 5.34 5.54 5.45 5.52 5.41

5.57 5.40 5.53 5.54 5.55 5.62 5.56 5.46 5.44 5.51

5.47 5.40 5.47 5.61 5.53 5.32 5.67 5.29 5.49 5.55

5.77 5.57 5.42 5.58 5.58 5.50 5.32 5.50 5.53 5.58

5.61 5.45 5.44 5.25 5.56 5.63 5.50 5.57 5.67 5.36

a. Construct a 99% confidence interval estimate of the population mean weight of the tea bags.

b. Is the company meeting the requirement set forth on the label that the mean amount of tea in a bag is 5.5 grams?

Solution. a.-) We don’t know the population variance, so we have to use the t-student distribution. Again, we have that the formula for the confidence interval is:

where is the sample mean, is the sample variance, and corresponds to the symmetric cut-off of the tail of the t-student distribution with degrees of freedom. Since, then

With the help of EXCEL we can compute the following table

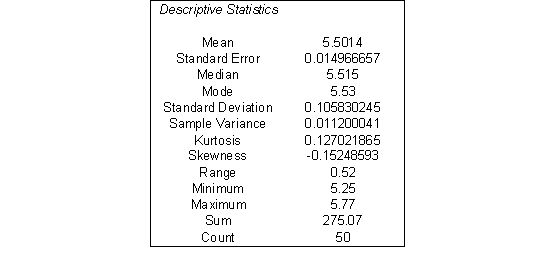
Therefore,, and . So, we compute the confidence interval as

Therefore, with probability 99%, the population mean satisfies

b.-) Given the information from a.-) we cannot be sure if the company is meeting the requirement set forth on the label. Even if the lower limit instead of being 5.462872 were greater that 5.5, still we couldn’t categorically say that the requirement is satisfied. Since is an unknown fixed parameter, we can only indicate if the evidence from the sample points in one direction or the other. There’s no evidence indicating that the company satisfy the requirement set forth on the label.

GO TO NEXT PROBLEM >>

Related Content