In the Box population experiment this year, the nominal 90% confidence interval using the simple random sample was independent
In the Box population experiment this year, the nominal 90% confidence interval using the simple random sample was independently constructed 27 times. Of these intervals, 24 included the true population mean. Let p be the true probability that this interval, based on a SRS and properly constructed, includes the true mean m.
a. Ignoring any concerns you may have with the Normal approximation, compute and interpret the approximate (Wald) 95% confidence interval for p.
b. Repeat problem (a) using the Agresti-Coull interval.
c. Obtain an exact 95% confidence interval for p, using Minitab’s one-sample proportion item under Stat Þ Basic Stat.
Solution: a. Wald’s approximate confidence interval is defined by
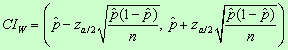
where 
corresponds to the critical value for the standard normal distribution for 
, 
is the sample proportion, and 
is the sample size. Plugging these values in the formula we obtain:
which corresponds to the 95% confidence interval for p. This means that this interval contains the true value of 
with approximately 95% confidence.
b. Agresti-Coull interval “adds two successes and two failures” to Wald’s interval. It’s defined as
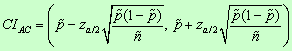
where again, 
and 
, which means that
c. Using Minitab we obtain
Related Content
Combining Efforts with a Statistics Expert - StatisticsHelp
The U.S. Weather Bureau has provided the following information about - StatisticsHelp
