Suppose a random sample of 85 items has been taken from a population and 40 of the sample can be characteristic of interest

Suppose a random sample of 85 items has been taken from a population and 40 of the sample can be characteristic of interest. Use this information to calculate a 90% confidence interval to estimate the proportion of the population that has the characteristic of interest. Calculate a 95% confidence interval. Calculate a 99% confidence interval. As the level of confidence changes and the other sample information stays constant, what happens to the confidence interval?

Solution: The 90% confidence level is

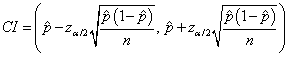
The sample proportion is

and the standard error:

  • For a 90% confidence interval we have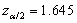, which means that the 90% confidence interval is (0.38153, 0.5596)
  • For a 95% confidence interval we have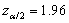, which means that the 95% confidence interval is (0.364476, 0.5767)
  • For a 99% confidence interval we have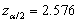, which means that the 99% confidence interval is (0.331127, 0.61005)

As we can see the width of the confidence interval increases as the confidence level increases.

GO TO NEXT PROBLEM >>

Related Content